כאשר מנתחים מבני נתונים ואלגוריתמים חשוב לדעת לא רק מה הם עושים אלא גם כמה משאבים הם צורכים. בפרק זה נלמד להעריך את יעילות האלגוריתם (כמה זמן וזיכרון הוא צורך בפועל) ולמדוד את סיבוכיותו – תיאור אסימפטוטי של התלות בגודל הקלט.
מה ההבדל בין יעילות לסיבוכיות?
הגדרת יעילות - מושג אמורפי שלא צריך לדעת
יעילות:(לא צריך לדעת) (Performance) בודקת את הזמן, הזיכרון ומשאבים אחרים שהאלגוריתם צורך במערכת מסוימת. למשל, כמה שניות לוקח לאלגוריתם לרוץ על מחשב ספציפי וכמה זיכרון RAM הוא משתמש. יעילות מושפעת מפרטי החומרה, שפת התכנות ומהמימוש.
סיבוכיות: מושג חשוב שצריך לדעת ונבחנים עליו
סיבוכיות היא מדד תאורטי המתאר כיצד זמן הריצה או השימוש במשאבים גדל עם גודל הקלט. סיבוכיות נמדדת לרוב ב‑Big‑O, המתארת חסם עליון אסימפטוטי – כלומר, איך האלגוריתם מתנהג כאשר גודל הקלט שואף לאינסוף. סיבוכיות אינה תלויה בפרטי החומרה.
סימון אסימפטוטי - ויקיפדיה \(Big\;O\;notation\)
בבגרויות חפשו את הצירוף תויכ (סוף המילה סיבוכיות, כתוב הפוך)
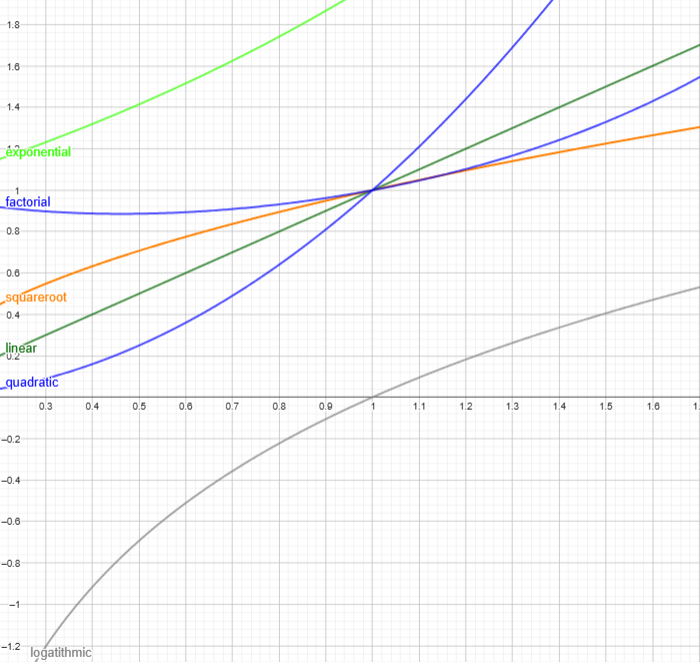
נתבונן בכמה פונצקיות ונסתכל איך הן גדלות
סיבוכיויות זמני ריצה נפוצות
א. \(O(1)\) – זמן קבוע: זמן הריצה אינו תלוי בגודל הקלט. למשל, גישה לאיבר במערך לפי אינדקס.
ב. \(O(log n)\) – לוגריתמית: פעולות שמקטינות את הבעיה פי שניים בכל צעד, כמו חיפוש בינארי.
ג. \(O(n)\) – ליניארית: זמן הריצה גדל ביחס ישיר לגודל הקלט – למשל מעבר על כל איברי המערך.
ד. \(O(n log n)\) – ליניארי לוגריתמי: אלגוריתמים מהירים למיון (כמו Merge Sort).
ה. \(O(n²)\) – ריבועית: אלגוריתמים שמבצעים לולאה בתוך לולאה (כמו Bubble Sort) או הדפסת ריבוע של כוכביות.
ו. גדולות יותר: \(O(2ⁿ)\) או \(O(n!)\) – בדרך כלל לא יעילים אלא אם הקלט קטן (כמו פיבונאצ’י או מגדלי הנוי ברקורסיה ללא Memoization)
התרשים משווה בין סיבוכיויות שונות. ככל שגודל הקלט n גדל, ההבדל בין \(O(n)\) לבין \(O(n^2)\) נהיה משמעותי.
אנליזה אסימפטוטית
כאשר אנו משתמשים ב‑Big‑O אנחנו מתעניינים בגרועה מבין האפשרויות (Worst‑Case). לפעמים ניתן לזהות גם מקרה ממוצע ו‑המקרה טוב. אך ההתייחסות היא תמיד למצב הגרוע ביותר.
כיצד לקבוע מה הסיבוכיות Big O
- שיטה כואבת - בהתחלה: נספור את הצעדים במדוייק ונגדיר פונקציית זמן ריצה. כמה צעדי חישוב נדרשים.
- בהמשך - נשאל את עצמנו כיצד זמן הריצה גדל כאשר הקלט גדל. האם היחס הוא לינארי (לדוגמא כאשר הקלט גדל פי 2 כמות הצעדים תגדל פי 2), או שהיחס הוא ריבועי? (כלומר, כאשר הקלט גדל פי 2 זמן הריצה יגדל פי 4 כמו בטיפול במערך דו מימדי ורוב המצבים בהם יש לולאה מקוננת)
- תמיד:
- נתחייחס למקרה הגרוע ביותר
- נתחשב בגורם המשפיע ביותר ונתעלם מהקבוע: למשל אם מספר הצעדים הוא \(5n^2+2n+7\) הסיבוכיות תהיה \(O(n^2)\). אם מספר הצעדים הוא \(3n\) הסיבוכיות היא \(O(n)\)
הגדרה לסיבוכיות זמן ריצה:
\(O(g(n))\) זמן ריצה שאינו עולה על הפונקציה \(g(n)\), עד כדי כפל בקבוע.
ניסוח נוסף: אינטואיטיבית, הביטוי \(O(g(n))\) מתאר את קבוצת הפונקציות שקצב הגדילה שלהן הוא לכל היותר זה של \(g(n)\)
הגדרה פורמלית
ניסוח קצת יותר פורמלי: הקבוצה \(O(g(n))\) הנה קבוצת כל הפונקציות \(f(n)\) כך ש \(f(n)\), עבור n גדול מספיק, חסומה מלמעלה ע”י \(c⋅g(n)\) עבור \(c>0\) כלשהו.
רישום מתמטי של ההגדרה הפורמלית:
\[\boxed{O(g(n))=\{f(n)|∃_{c>0,n_{0}>0}∀_{n≥n_{0}}f(n) \leq c·g(n)\}}\]למה הנושא הכללי נקרא אסימפטוטיקה?
דוגמה: השוואת לולאה אחת ולולאה כפולה
נבחן שתי פונקציות שמחשבות סכום של מטריצה מרובעת בגודל n × n. הראשונה משתמשת בלולאה כפולה והשנייה משתמשת בלולאה אחת.
// O(n²) סכום מטריצה בשתי לולאות מקוננות – סיבוכיות
public static int SumMatrixNested(int[,] matrix)
{
int sum = 0;
for (int i = 0; i < matrix.GetLength(0); i++)
{
for (int j = 0; j < matrix.GetLength(1); j++)
{
sum += matrix[i, j];
}
}
return sum;
}
// O(n) סכום מערך חד-ממדי – סיבוכיות
public static int SumArray(int[] row)
{
int sum = 0;
for (int i = 0; i < row.Length; i++)
{
sum += row[i];
}
return sum;
}
הפונקציה הראשונה מבצעת \(n^2\) חיבורי איברים ולכן יש לה סיבוכיות ריבועית, כלומר, \(O(n²)\). הפונקציה השנייה עוברת על מערך חד-ממדי ולכן היא בסיבוכיות לינארית, כלומר, \(O(n)\)
אורך הקלט: את הסיבוכיות יש לרשום תמיד עם n, כלומר יש לרשום תמיד \(O(n), O(n²), O(\log n)\), אבל חשוב להגדיר מהו אורך הקלט. מהו n
ברישום סיבוכיות תמיד מתבטאים במונחי n בלי קשר לשמות המשתנים.
כך למשל עבור פונקציה סוכמת int Sum(arr[]) הסיבוכיות היא \(O(n)\) אך בנוסף יש לציין ש-\(n\) הוא אורך המערך arr
טבלה – קישור בין אלגוריתמים לסיבוכיות
| אלגוריתם | סיבוכיות ריצה | הערות |
|---|---|---|
| חיפוש ליניארי | O(n) | מעבר על כל האיברים עד שמוצאים ערך מסוים |
| חיפוש בינארי | O(log n) | דורש מערך ממויין, חוצה את הטווח לשניים בכל צעד |
| מיון בחירה | O(n²) | שתי לולאות לקביעת מינימום בכל איטרציה |
| Merge Sort | O(n log n) | מחלק את הקלט, ממזג ומחלק שוב |
| מיון בועות | O(n²) | ביצוע החלפות בין איברים סמוכים |
דוגמא לשאלה הנפתרת בלולאה מקוננת בסיבוכיות לינארית \(O(n)\)
נתון מערך לא ממויין של מספרים שלמים. עליכם לבדוק האם קיים תת-רצף רציף (subarray) אשר סכום האיברים בו שווה למספר נתון target.
דרישות השאלה:
- כתבו פונקציה המקבלת
int[] arr, מספרint targetומחזירהboolהאם קיים תת-רצף רציף שסכומו שווהtarget. - הפונקציה צריכה להשתמש בלולאת
whileחיצונית ולולאה פנימית כדי להזיז את החלון. - זמן ריצה: O(n).
מימוש אפשרי: לולאת while שמזיזה את תחילת החלון (start) ולולאה פנימית while שמזיזה את סוף החלון (end), עם הגדלות של התחום כך שסכום החלון מתקרב/חורג מ-S. השיטה הזו משתמשת בלולאות מקוננות (outer ו-inner), אבל כל איבר במערך נבדק/מוזז בסך הכול מספר קבוע של פעמים—לכן זמן הריצה הכולל הוא \(O(n)\) ולא \(O(n²)\).
פתרון אפשרי
// בודקת אם קיים תת-רצף רציף שסכומו == target
public static bool HasSubarrayWithSum(int[] arr, int target)
{
int n = arr.Length;
int start = 0, end = 0, currentSum = 0;
while (start < n)
{
// n לא עבר את הגבול end וה- target -כל עוד הסכום קטן מה
while (end < n && currentSum < target)
currentSum += arr[end++]; // end -נוסיף לסכום ונזיז את ה
if (currentSum == target) // אם הגענו לסכום בדיוק target — הצלחה
return true;
// כדי לקדם את החלון start הסכום גדול מהנדרש לכן נקטין אותו ונזיז את
currentSum -= arr[start++];
}
return false; // ברירת מחדל: לא הצלחנו למצוא
}
static void Main()
{
int[] arr = { 1, 4, 20, 3, 10, 5 };
int S = 33;
Console.WriteLine(HasSubarrayWithSum(arr, S)); // כן — למשל 20+3+10 = 33
}
ניתן לעיתים לפצח את הבעיה ללא קינון.
דוגמא כמעט מושלמת לפתרון כזה. מה לא בסדר - מתי הדוגמא תיכשל וכיצד יראה פתרון נכון?
public static bool HasSubarrayWithSum2(int[] arr, int target)
{
int n = arr.Length;
int start = 0, end = 0, currentSum = 0;
while (start < n && end <= n)
{
if (currentSum < target && end<n)
currentSum += arr[end++]; // נוסיף איבר חדש ונקדם את end
else if (currentSum > target)
currentSum -= arr[start++]; // הסכום גדול מדי — נזיז את start קדימה
else // currentSum == target
return true; // הצלחה
}
return false; // לא נמצא תת-רצף
}
דוגמא נכונה תימסר לפי דרישה.
כדי לבדוק נכונות יש:
- לאתחל מספר מערכים שונים שנבחרו בקפידה עם סכומים מתאימים או לא מתאימים
- לבצע Debug.Assert(HasSubarrayWithSum(ar,s) == HasSubarrayWithSum2(ar,s))
הסבר למה הפתרון הוא O(n)
- כל אינדקס
startו-endנע קדימה לאורך המערך, ולא חוזר אחורה. - בלולאה החיצונית
startרץ מ-0 עד n-1 כמקסימום. - בתוך הלולאה הפנימית,
endגם כן רץ מ-0 עד n-1 לכל היותר, אך ל-end אין “איפוס” לאחר כל התחלה — הוא רק מתקדם. - לכן כל איבר במערך נכלל ונשלף מחלון בסך הכל פעם אחת (או מספר קבוע של פעמים), כך שהסך הכולל של הפעולות הוא פרופורציונלי ל-n \(O(n) ⟵\).
דוגמא נוספת לקינון בסיבוכיות לינארית
נתון מערך של מספרים שלמים. נגדיר רצף זהים כקטע רציף במערך שבו מופיע אותו ערך לפחות פעמיים ברצף. לדוגמה, במערך:
1, 5, 2, 2, 7, 3, 3, 3
קיימים שני רצפים:
- הרצף של
2, 2 - הרצף של
3, 3, 3
כתבו פונקציה המקבלת מערך ומחזירה את מספר הרצפים.
הפתרון ייעשה בעזרת לולאת while מקוננת, אך באופן שבו כל איבר במערך נבדק לכל היותר פעם אחת — ולכן זמן הריצה יהיה לינארי O(n).
פתרון
public static int CountEqualRuns(int[] arr)
{
int n = arr.Length;
int i = 0, runs = 0;
while (i < n - 1) // צריך לפחות שני איברים כדי ליצור רצף
{
if (arr[i] == arr[i + 1])
{
runs++; // מצאנו התחלה של רצף
// נתקדם בלולאה פנימית עד סוף הרצף
while (i < n - 1 && arr[i] == arr[i + 1])
i++;
}
i++; // תמיד מתקדמים צעד אחד קדימה
}
return runs;
}
דוגמה להרצה
int[] arr = { 1, 5, 2, 2, 7, 3, 3, 3 };
Console.WriteLine(CountEqualRuns(arr)); // התוצאה: 2
למה זה O(n)?
- הלולאה החיצונית רצה על המערך.
- הלולאה הפנימית “קופצת” קדימה על פני רצפים שלמים של איברים זהים.
- כל איבר נבדק לכל היותר פעמיים (בבדיקה מול השכן ובדילוג), ולכן הסיבוכיות הכוללת היא לינארית.
מדוע פיבונאצ’י והאנוי הם בסיבוכיות אקספוננציאלית \(O(2ⁿ)\)?
להרחבה בנושא זיהוי סיבוכיות מעריכית
סדרת פיבונאצ’י (מימוש נאיבי ברקורסיה)
ההגדרה הרקורסיבית היא:
\[F(n) = \begin{cases} 0 & n=0 \\ 1 & n=1 \\ F(n-1) + F(n-2) & n>1 \end{cases}\]- כל קריאה מייצרת שתי קריאות רקורסיביות (חוץ מהמקרים הבסיסיים).
- עץ הקריאות גדל בקצב מעריכי.
👈 סיבוכיות זמן: \(O(2^n)\)
מגדלי האנוי (רקורסיבי, ללא אופטימיזציות)
האלגוריתם הרקורסיבי:
- מעבירים \(n-1\) דיסקים למוט עזר.
- מעבירים את הדיסק הגדול ביותר למוט היעד.
- מעבירים שוב \(n-1\) דיסקים ממוט העזר למוט היעד.
הנוסחה הרקורסיבית היא:
\[T(n) = 2\cdotT(n-1) + 1\]הפתרון הוא:
\[T(n) = 2^n - 1\]👈 סיבוכיות זמן: \(O(2^n)\)
תרגול וקישורים
כדי לתרגל ניתוח סיבוכיות, נסו לדרג את הסיבוכיות של פונקציות שאתם כותבים בתרגולים הבאים. התרגולים יפתחו במערכת ההגשות:
אתגר
כתבו פונקציה שמאתרת במערך דו‑ממדי את הערך המקסימלי שקיים בדיוק במחצית מהשורות. נסו לנתח את סיבוכיות הפונקציה שהגדרתם.